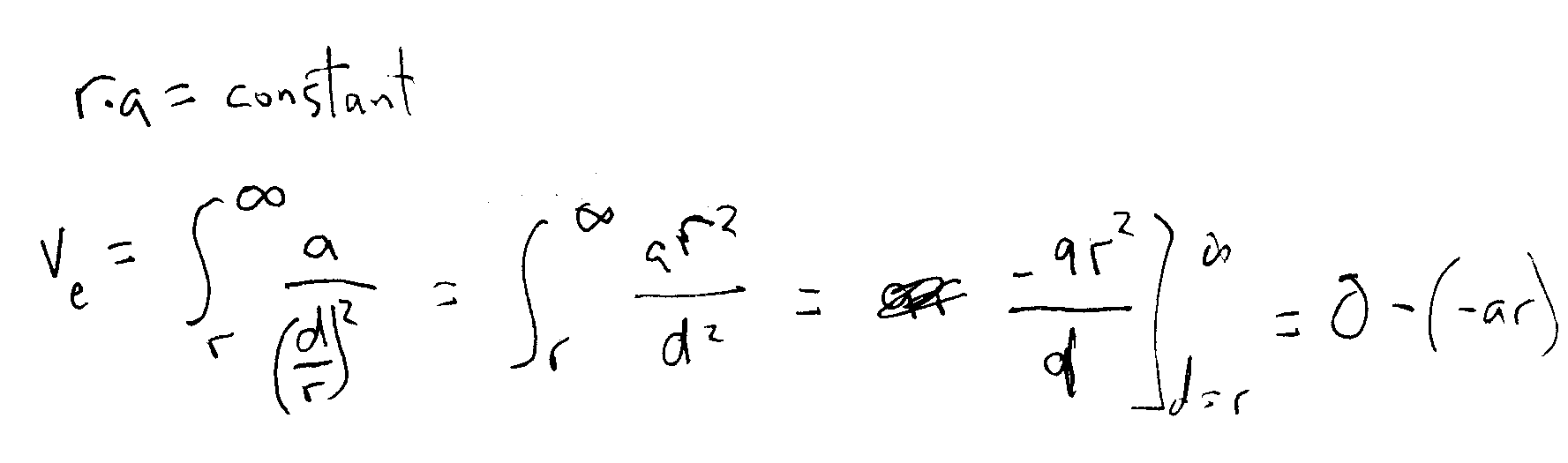Black holes – or more specifically, their event horizon – are a cosmic mirage. Not much different from a rainbow. Oh, they’re real alright, I’m not talking about leprechauns with the pot of gold at the end, but the way we experience them is totally different from the thing itself. There is no such thing as “falling though the event horizon” because the “event horizon” is precisely only our experience of it.
Contradictions in last episode
The interesting thing about scientific inquiry is you’re never satisfied with your answers. Answers always lead to contradictions, things that don’t make sense, new questions. I had answered how something can accelerate to light speed in a black hole’s pull. But what if it doesn’t? What if some daring astronomer constantly decelerates himself as he comes closer and closer to the event horizon, constantly making sure he’s both aiming for dead center, and making a nice slow descent?
Now you could counter by saying that if you didn’t let yourself freefall, the G forces would tear you to shreds. But here comes the complicating factor. Supermassive black holes exist which have relatively weak gravitational force at the event horizon. A black hole with a radius of about one light year, for example, would have a gravitation at its event horizon equivalent to here on Earth’s surface (aka 1G).
Not so coincidentally, if you were to accelerate for about a year at 1G, you would reach what I call nominal light speed – which is your actual speed if you accelerated to light speed in a simplified Newtonian universe That just happens to be 0.618c (0.618 the speed of light) – which is exactly the proportion of the golden rectangle (?) – but we’ll save this tidbit for later. The question right now is how is such weak gravity at an event horizon even possible? Aren’t black holes supposed to spaghettify us and tear us into subatomic shreds and stuff?
What’s an event horizon doing with such, well, EARTHLY gravity?
Wait, what?
Yes, that’s right.  Supermassive black holes have very low gravity at their event horizon. It’s a simple formula, really. The radius of the event horizon is the inverse of its acceleration – i.e. gravity. r*a is the same for each and every black hole.
Supermassive black holes have very low gravity at their event horizon. It’s a simple formula, really. The radius of the event horizon is the inverse of its acceleration – i.e. gravity. r*a is the same for each and every black hole.
I could do some extra wizardry to show you the math, but you have the internet for that. Small black holes pull really hard on that photon to whip it in a circle. Large black holes can take their sweet time. And here’s the fun part – if you were to free-fall into a black hole 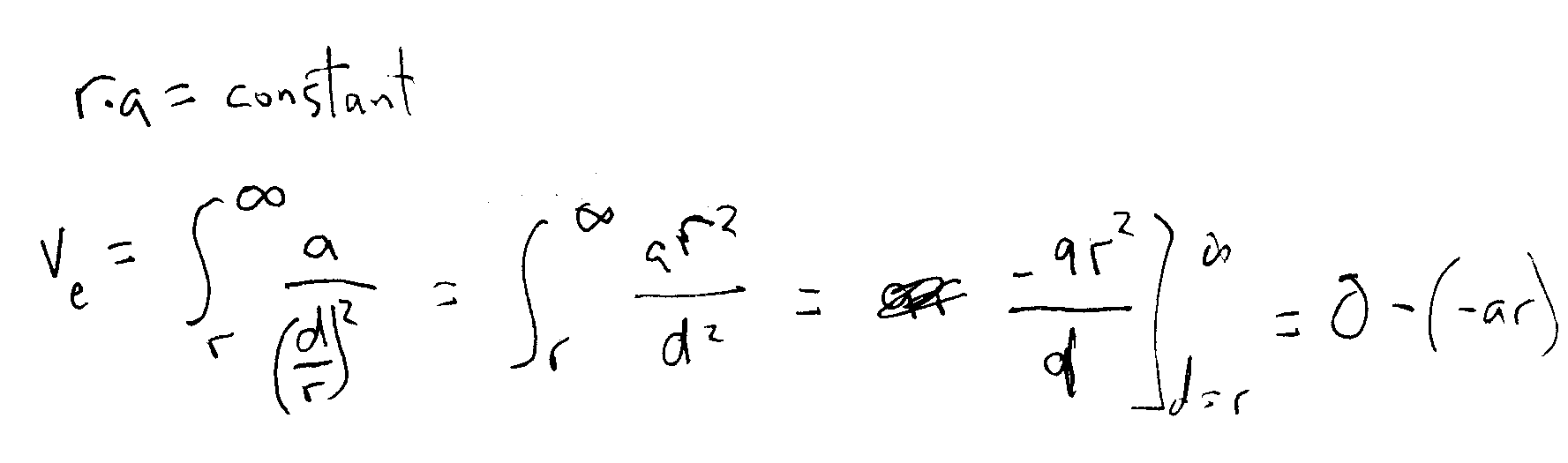 – ANY black hole – from somewhere outside its influence, you’d accelerate to the speed of light. Ve = velocity at event horizon = c (speed of light).
– ANY black hole – from somewhere outside its influence, you’d accelerate to the speed of light. Ve = velocity at event horizon = c (speed of light).
But the twisted logic that happens at that event horizon remains the same.
A lesson on geodesics
Well, how do we wrap our minds around that?
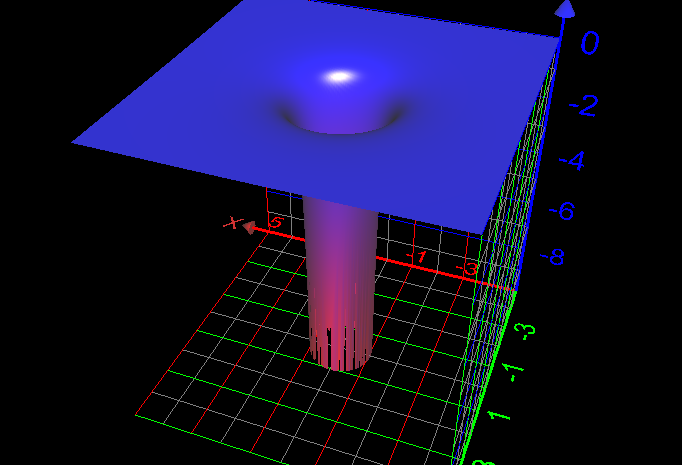
The non-euclidean geometry (geodesics) of a black hole, as discussed in our previous post
For that we have to delve into the world of geodesics. And first in that, a beef. I don’t like the term “geodesics.” It conjures up hippy domes in the middle of the desert. I prefer the term “non-Euclidean geometry”. It easily tells us we’ve left the familiar world of ancient geometers with their simple circles and triangles on a flat surface, and are falling down the rabbit-hole (so to speak) of curved spaces and planes.
And that’s what we need to know to understand a blackhole. It’s how we can picture Einstein’s theory of relativity. If you’ll recall from my last post, this 3D well describes the spacetime around a black hole – how it curves down into an infinite well.
There’s a few things going on in that diagram, so we’ll try to take it a bit at a time.
The thing to remember about this well is, it’s not like gravity is pulling everything down it. It mainly describes how light, a massless particle that always travels in a perfectly straight line, can still seem to bend.
Now there’s difference in the specifics of how light and massive entities fall towards a gravitational center. But what’s the same is the acceleration. Here on Earth, we are constantly accelerating towards it at 9.8m/s2. And light is no different.
Even though it travels in a straight line.
And that’s my second beef with “geodesics” – the definition of a straight line as the closest distance between two “local” (i.e. “close”) points. That’s a bit of a copout, like saying “well we’re reducing this to a map”. I prefer the term “no sideways pull”.
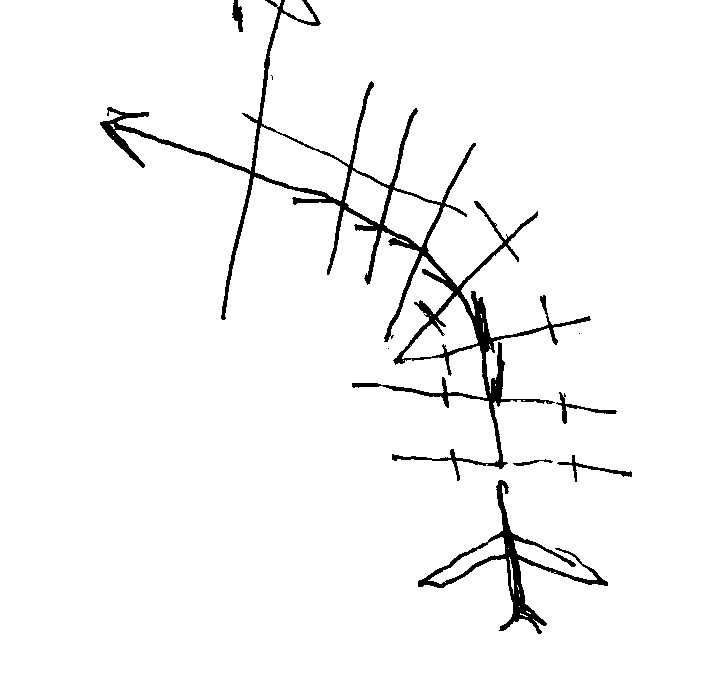
The (air)plane rotates, twisting the (geometric)plane it’s on, and then lifts into a turn. Get it?
But let’s go back to our analogy of the plane from last chapter. There’s rudderless planes out there. By just rotating the plane with ailerons, and using the elevators in back, you can turn every which way without ever having sideways pull. Just rotate the plane, and go up or down.
So if you look at what makes the plane “turn without turning”, the factor here is “which way is up”. As it rotates, it changes that “upwards” direction, and then goes up or down in that upwards direction.
And BTW, this works equally for spaceships in zero gravity. So gravity has nothing to do with which way is up. In more complicated math, it’s called “orthogonal” which is defined as the perpendicular to the plane. This allows us to pile on more dimensions.
But we’re here to discuss black holes, not study math. So let’s translate this “upness” into black holes. 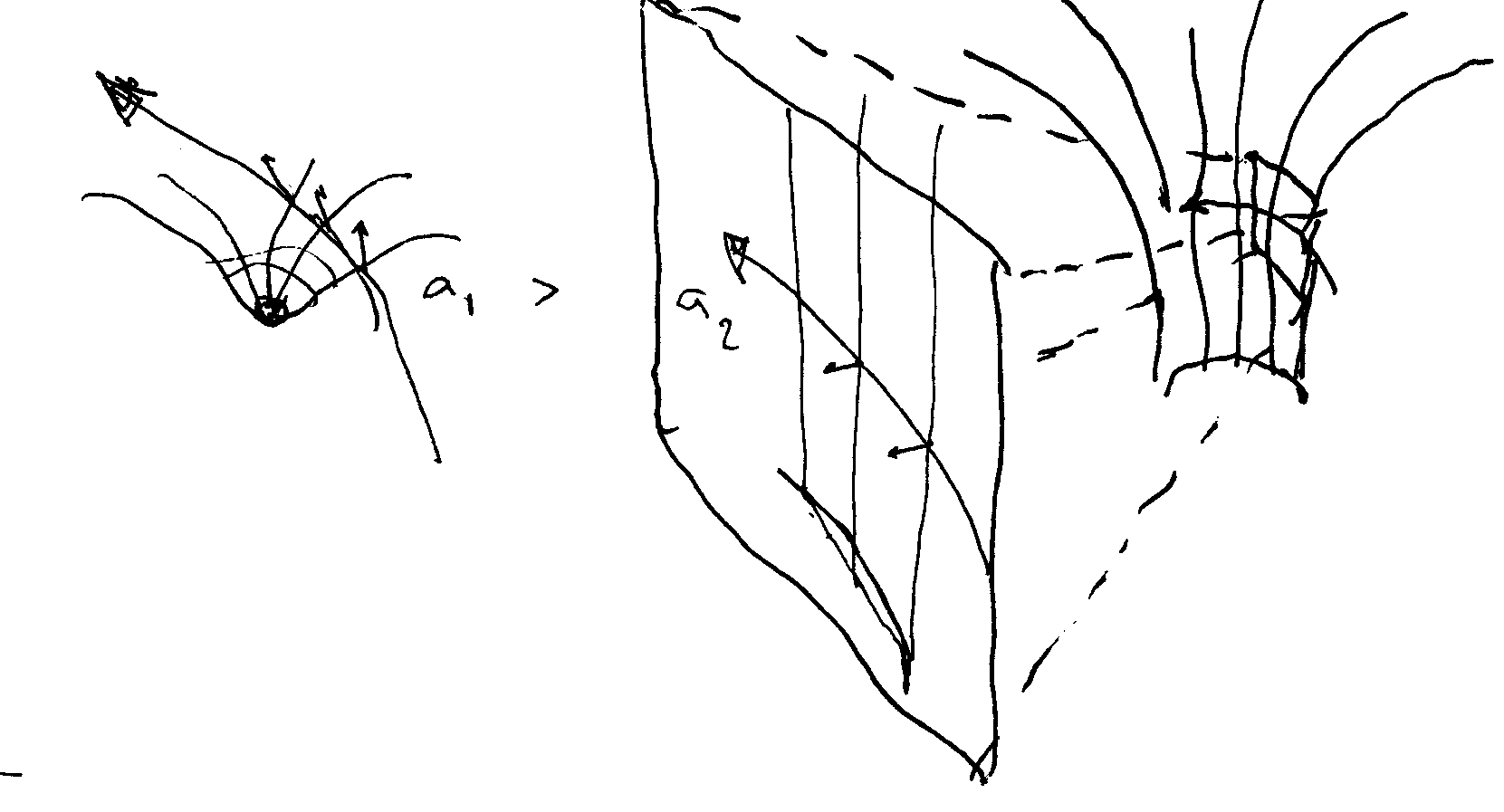 Compare Earth’s gravitation of a beam of light – a1 – and compare it with a REALLY massive black hole, whose acceleration near the event horizon is less than at Earth’s surface.
Compare Earth’s gravitation of a beam of light – a1 – and compare it with a REALLY massive black hole, whose acceleration near the event horizon is less than at Earth’s surface.
As a light beam approaches earth, it enters Earth’s gravity, changing its “upness” and starts to “curve” around Earth. What causes the curve is the “upness changing”.
Now, compare that to a supermassive black hole. By the time you’re near the event horizon (as seen by this incredibly drawn cut-out) you’re practically vertical. But there’s not much “upness” left to change. You’re just being whipped around in what seems like a flat surface, in a very large cylinder, “upness” pointing directly into the middle.
Any way you look at it, it’s the speed of light
The problem though, with such small scale cutouts, is they conveniently leave out just how far we’ve come to get to this “vertical space” in the supermassive black hole. As I hinted earlier, before we get to this spot in a supermassive black hole, we’d have been freefalling literally for years and years.
But what if we decided not to freefall? What if we got some theoretical rocket thrusters and slowed down our descent, so we avoided being anywhere near the speed of light at the event horizon?
Einstein’s Theory of Gravitation
The answer is it doesn’t matter. Because how would you do that? You would manually accelerate yourself in this gravitational field. If you did the same manual acceleration outside a gravitational field (i.e. deep space), you would go from 0 to light speed. So no matter what your behavior is around the event horizon – hovering, freefalling, or some combination of the two (i.e. orbiting) – you’d be at near light speed.
This is what Einstein is talking about, that we experience a spacetime dilation in a gravitational field, even if we’re hovering/standing/using rocket thrusters. The spacetime dilation is basically equal to the sum of acceleration from deep space to whatever surface you’re at.
Back to where we started
Which takes us back to the incredible shrinking black hole, except this time we take it a step further. In the last post, we talked about the fact that a black hole shrinks away from any object approaching it. But just how? We don’t want to just WATCH something fall into a black hole, we want to KNOW what it’s like. We want to BE whatever it is that falls in.
Well, considering we nixed any realistic possibility of crossing the event horizon with strange tricks, let’s pretend we’re freefalling directly to a black hole’s heart. And orbits are boring. We want to go straight in. So we have this craft that doesn’t try to resist gravity, and doesn’t let us slip to the right or left. And we’ll start well outside a nice supermassive black hole, about 1 light year diameter.
The best way to picture this is pretend we’re falling in a Newtonian universe, and at periodic intervals, we’ll recalibrate to allow for how spacetime changed around us. Don’t worry, if someone gives us flak for this, just tell them delta apporoaches zero. If it doesn’t shut them up, send them my way.
If you were to freefall to what you think is the event horizon, you’d hit what you’d think was light speed in a Newtonian universe – i.e. “nominal light speed”, or to put it another way, Newtonian velocity = momentum divided by mass = light speed (v=p/m=c). So let’s take our new bearings.
Distance to center is still r.
Actual relativistic speed is now ?c (~.618c).
At ?c, distances shrink to ??. So the radius of the new black hole is r*??.
Time also dilates to ?(1+?) for those outside of you, but we don’t care about them, so that’s kind of irrelevant.
Recalibrate your instruments for your new reality, and freefall AGAIN to “nominal light speed” – the speed you’d reach at the new event horizon at r*??.
Distance to center is now r*??.
Except now you’re at ?c compared to where you were before, or basically, your momentum doubled from your starting point. You’re at ?c compared to your last point. Or, to put It another way, Newtonian velocity is twice the speed of light (p/m=2c).
New event horizon is now r*?.
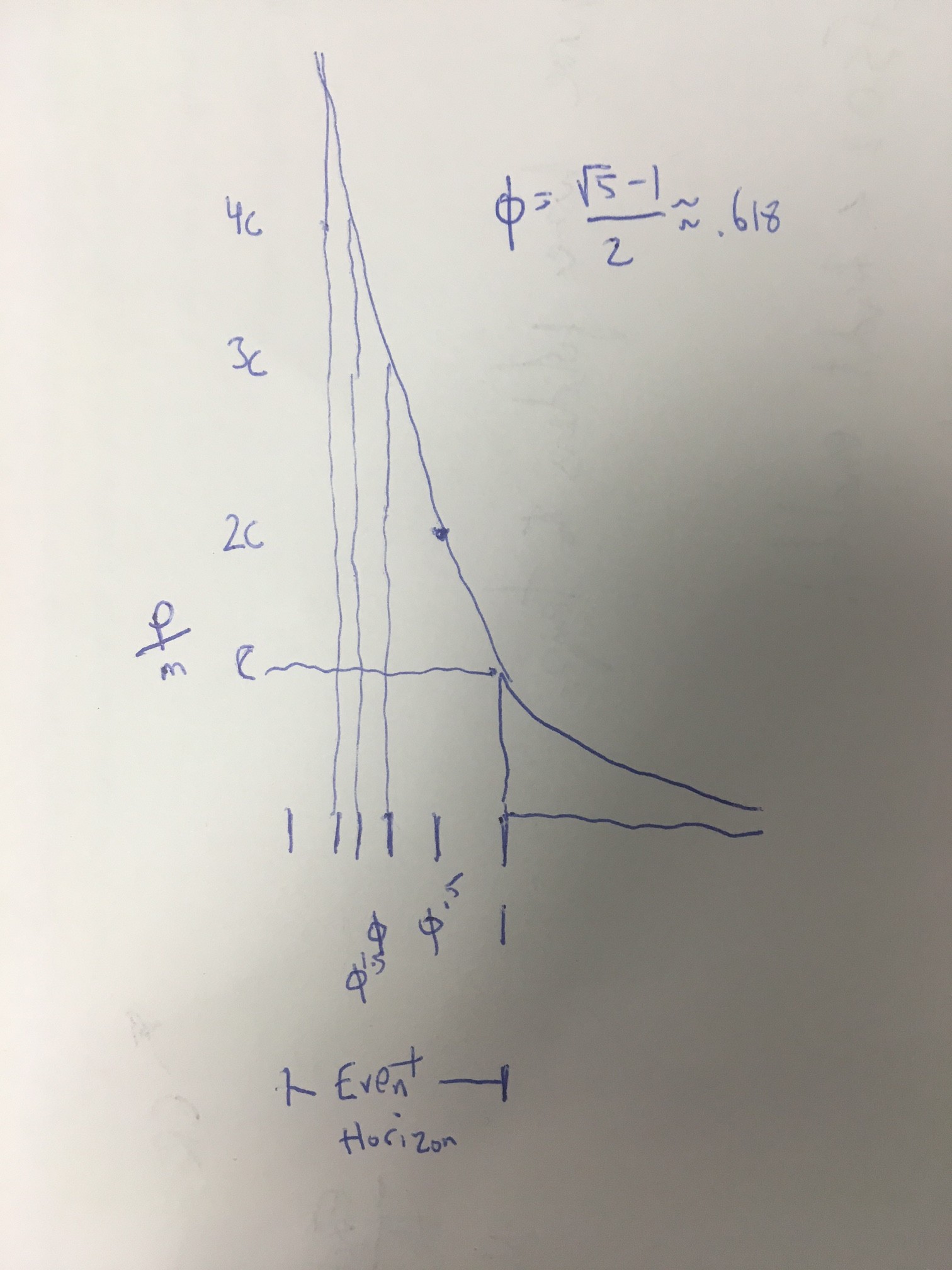
While “light speed” is maximum, momentum is infinite. Here’s how momentum compares to the relative size of an event horizon. You would even out where the event horizon was ?? times the distance from the singularity as you are.
And so on, in the grand progression of the golden rectangle. The ultimate equation is that y=r*a/ ?0.5(x-1) . Where y is your Newtonian velocity (momentum/mass) and x is the radius of the black hole.
Here, you know what? Let’s draw a graph.
Notice there’s no time here. Acceleration is whatever it is to get you to the light speed you’d reach at event horizon.
How far down do you want to go? How much can your imaginary ship take? How infinitely fast do you want to go? How far do you want to escape those boring confines of flat spacetime and see the universe from the perspective of the infinite?
That is what it’s like to fall down that well.