It started with a simple graph: the rotation of the function y=1/(x2+y2-h2). I didn’t quite know what the metric was for a black hole, but I knew I was close. The familiar well came up, with an asymptotal cylinder of radius h. But something else happened. I forgot it also had a “goblet” in the middle.
My more formal mathematical training taught me to throw that goblet away and deal with the “real” and “finite world outside of a black hole’s event horizon. Then I read about Rahmanujan. Why exactly do we throw these away, anyway? Don’t they tell us something?
Rahmanujan has gained some importance recently, because the peculiar thing about black holes is they touch infinity at the event horizon. So his mathematics of infinity, of throing away this self-imposed limit on our math, would seem to give us some insights.
But it goes further than that. Could there be a “negative world” inside the event horizon? And would it be really all that negative?
How event horizons differ from planet surfaces
Take two planets of equal density. Collide them together to make a new planet that’s still perfectly round. The new radius will be 3root2 or ~1.26 times the old radius.
But what happens to the event horizon of two colliding black holes of the same radius? The new radius will be double the old radius. Why is that? That’s because an event horizon is nothing like a planet surface, it is the radius at which light makes a perfect circle around a black hole. So the larger the radius, the less light needs to accelerate. Turns out that once the calculations are done, the radius of a black hole is directly proportional to its mass, and not the cube root like a planet.
This means that the larger black holes get, the less dense they need to be.
Black Hole Sea
We keep talking about black holes as some dramatic star crushing into a singularity, like that’s all they can be. But so long as any matter of any form and any volume can pull light into an orbit around itself, it will “cloak” itself in an event horizon. The second thing to remember is black holes are really small. A typical stellar black hole will only be a few kilometers across. Compare that to the Earth which is over ten thousand kilometers across.
So a black hole with the density of Mercury’s orbit will have the density of our atmosphere.
What then, about nebulas? While a nebula is only about a thousandth(?) times as dense as our atmosphere, remember you double the radius and you 2^3 volume, so you only need 1/8 the density. Black holes get rarefied really quickly. A nebula the size of our solar system could well be a black hole candidate.
Now that we’re predicting supermassive black holes at the center of galaxies, that very well may be how these guys have spawned.
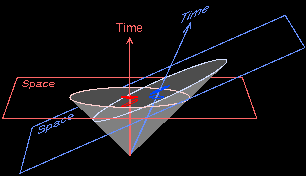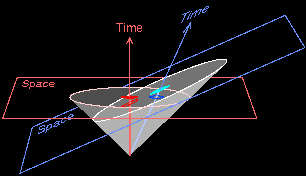
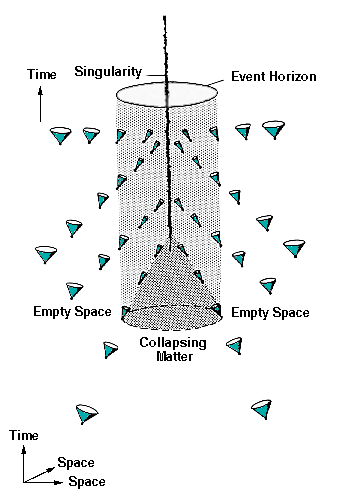
But what of the matter on the inside? We can’t imagine that anything spectacularly instant would happen to the matter. So it means we have this matter, which creates an event horizon, and still has a very nicely independent existence from the world outside of it. But then if it’s inside the event horizon, and is still curving spacetime the same way, it should very well curve (carve?) out this goblet shape that asymptotes to a cylinder at the evnet horizon.
The Universe inside a Black Hole
Here’s where it gets really interesting. As an event horizon increases, the density decreases. Turns out that the entire mass of the universe can generate an event horizon that’s about the size of the known universe. And here’s the thing. A goblet shape will create “anti-gravity”. Everything inside the goblet will slowly slide towards the event horizon on the perimeter.
And so we just found a novel way to explain accelerating expansion.
It’s counterintuitive to think of us being in a black hole when we associate it with such powerful tidal forces and gravitation. But if you think of an event horizon that’s billions of light years across – that means light only carves a circle once every few dozen billion years. The acceleration would be negligible to even our most delicate instruments.
And considering light is timeless and dimensionless, it really doesn’t care whether it carves out a circle of a few kilometers of a few billion light years. Its path is just as instant and timeless. And so the curvature should not care either.
The Parallax Paradox – why a goblet appears flat to us
But we still have to account for the fact that, by our best instruments, the universe appears to have flat curvature. But how do we know this? We do it by measuring a large flat “parallax triangle” and seeing if the sides add up to 180 degrees. If it ‘s less or more, we know it’s curved.
The problem is, plenty of shapes will still give us 180 degrees. A cylinder, for one. Which is what a goblet asymptotes into. So we could very well be drawing this triangle that simply follows a curve path along the goblet that still gives us 180 degrees.